https://www.acmicpc.net/step/8
일반 수학 1 단계
벌집이 형성되는 규칙에 따라 벌집의 위치를 구하는 문제
www.acmicpc.net
백준 / 2745번
문제
B진법 수 N이 주어진다. 이 수를 10진법으로 바꿔 출력하는 프로그램을 작성하시오.
10진법을 넘어가는 진법은 숫자로 표시할 수 없는 자리가 있다. 이런 경우에는 다음과 같이 알파벳 대문자를 사용한다.
A: 10, B: 11, ..., F: 15, ..., Y: 34, Z: 35
입력
첫째 줄에 N과 B가 주어진다. (2 ≤ B ≤ 36)
B진법 수 N을 10진법으로 바꾸면, 항상 10억보다 작거나 같다.
출력
첫째 줄에 B진법 수 N을 10진법으로 출력한다.
풀이
-Python3
N, B = input().split()
print(int(N, int(B)))다른 언어였으면 B^자릿수 * N 의 총합을 구하면서 복잡해졌을 것 같은데, 파이썬에서는 int 함수를 사용해 간단히 구현 가능하다. int(A, B) 는 B진수법으로 적힌 A를 십진수 int형으로 리턴하기 때문이다.
백준 / 11005 (★)
문제
10진법 수 N이 주어진다. 이 수를 B진법으로 바꿔 출력하는 프로그램을 작성하시오.
10진법을 넘어가는 진법은 숫자로 표시할 수 없는 자리가 있다. 이런 경우에는 다음과 같이 알파벳 대문자를 사용한다.
A: 10, B: 11, ..., F: 15, ..., Y: 34, Z: 35
입력
첫째 줄에 N과 B가 주어진다. (2 ≤ B ≤ 36) N은 10억보다 작거나 같은 자연수이다.
출력
첫째 줄에 10진법 수 N을 B진법으로 출력한다.
풀이
-Python3
N, B = map(int, input().split())
result= ""
number = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
while N:
result += str(number[N%B])
N //= B
print(result[::-1])B진법으로 만든다 = B로 계속해서 나눈다 를 이해해야 풀 수 있음...
-들어온 수 N을 B로 나눈 결과를 계속해서 결과 변수에 저장하면 된다.
-이때 B는 한자릿수 이상일 수 있고, 그 경우 미리 선언된 대문자 알파벳까지 이어지게 된다.
-int형 그대로를 저장할시 덧셈을 해버릴 수 있기 때문에 result로 저장하기 전 str() 함수로 스트링 변환해준다.
-들어온 수 N은 반복될 때마다 나머지로 다시 저장한다.
이때 연산한 건 1의자릿수부터기 때문에 역순으로 출력해야 하는 것을 조심!!
백준 / 2720번
문제
미국으로 유학간 동혁이는 세탁소를 운영하고 있다. 동혁이는 최근에 아르바이트로 고등학생 리암을 채용했다.
동혁이는 리암에게 실망했다.
리암은 거스름돈을 주는 것을 자꾸 실수한다.
심지어 $0.5달러를 줘야하는 경우에 거스름돈으로 $5달러를 주는것이다!
어쩔수 없이 뛰어난 코딩 실력을 발휘해 리암을 도와주는 프로그램을 작성하려고 하지만, 디아블로를 하느라 코딩할 시간이 없어서 이 문제를 읽고 있는 여러분이 대신 해주어야 한다.
거스름돈의 액수가 주어지면 리암이 줘야할 쿼터(Quarter, $0.25)의 개수, 다임(Dime, $0.10)의 개수, 니켈(Nickel, $0.05)의 개수, 페니(Penny, $0.01)의 개수를 구하는 프로그램을 작성하시오. 거스름돈은 항상 $5.00 이하이고, 손님이 받는 동전의 개수를 최소로 하려고 한다. 예를 들어, $1.24를 거슬러 주어야 한다면, 손님은 4쿼터, 2다임, 0니켈, 4페니를 받게 된다.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 거스름돈 C를 나타내는 정수 하나로 이루어져 있다. C의 단위는 센트이다. (1달러 = 100센트) (1<=C<=500)
출력
각 테스트케이스에 대해 필요한 쿼터의 개수, 다임의 개수, 니켈의 개수, 페니의 개수를 공백으로 구분하여 출력한다.
풀이
-Python3
T = int(input())
while T :
C = int(input())
Quarter = C//25
Dime = C%25//10
Nickel = C%25%10//5
Penny = C%25%10%5
print(Quarter, Dime, Nickel, Penny)간단한 거스름돈 프로그램...
달러의 100배인 센트로 입력하기 때문에 쿼터(25), 다임(10), 니켈(5), 페니(1)로 나눠서 각 개수를 출력하면 된다.
공백으로 구분하여 출력
좀 무식한 하드코딩인가?
백준 / 2903번
문제
상근이는 친구들과 함께 SF영화를 찍으려고 한다. 이 영화는 외계 지형이 필요하다. 실제로 우주선을 타고 외계 행성에 가서 촬영을 할 수 없기 때문에, 컴퓨터 그래픽으로 CG처리를 하려고 한다.
외계 지형은 중앙 이동 알고리즘을 이용해서 만들려고 한다.
알고리즘을 시작하면서 상근이는 정사각형을 이루는 점 4개를 고른다. 그 후에는 다음과 같은 과정을 거쳐서 지형을 만든다.
- 정사각형의 각 변의 중앙에 점을 하나 추가한다.
- 정사각형의 중심에 점을 하나 추가한다.
초기 상태에서 위와 같은 과정을 한 번 거치면 총 4개의 정사각형이 새로 생긴다. 이와 같은 과정을 상근이가 만족할 때 까지 계속한다.
아래 그림은 과정을 총 2번 거쳤을 때까지의 모습이다.
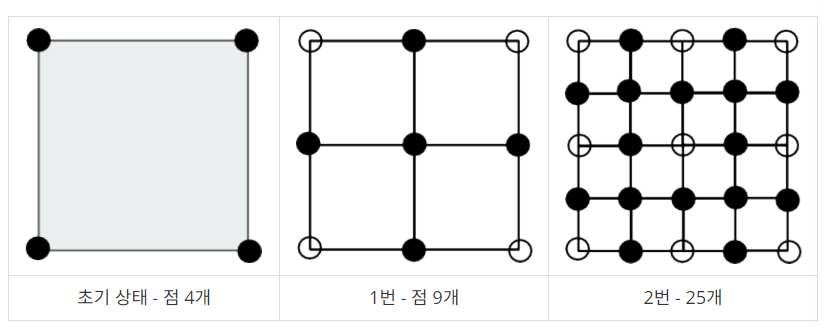
상근이는 어떤 점은 한 개 보다 많은 정사각형에 포함될 수 있다는 사실을 알았다. 메모리 소모량을 줄이기 위해서 중복하는 점을 한 번만 저장하려고 한다. 과정을 N번 거친 후 점 몇 개를 저장해야 하는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N ≤ 15)
출력
첫째 줄에 과정을 N번 거친 후 점의 수를 출력한다.
풀이
-Python3
print((2**int(input())+1)**2)반복이 있는 문제는 차라리 입출력을 보고 알고리즘을 단순화하는 게 나은 것 같다
이 경우에 (2^n+1)^2라는 규칙이 존재하기 때문에 간단히 해결할 수 있다.
백준 / 1193번(★)
문제
무한히 큰 배열에 다음과 같이 분수들이 적혀있다.
| 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | … |
| 2/1 | 2/2 | 2/3 | 2/4 | … | … |
| 3/1 | 3/2 | 3/3 | … | … | … |
| 4/1 | 4/2 | … | … | … | … |
| 5/1 | … | … | … | … | … |
| … | … | … | … | … | … |
이와 같이 나열된 분수들을 1/1 → 1/2 → 2/1 → 3/1 → 2/2 → … 과 같은 지그재그 순서로 차례대로 1번, 2번, 3번, 4번, 5번, … 분수라고 하자.
X가 주어졌을 때, X번째 분수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 X(1 ≤ X ≤ 10,000,000)가 주어진다.
출력
첫째 줄에 분수를 출력한다.
풀이
-Python3
print((2**int(input())+1)**2)컴퓨터 알고리즘 교재에서 비슷한 문제를 본 것 같은데 어렵다
알고리즘 공부 좀 해야지..
규칙찾기가 너무 어려웠다
N = int(input())
line = 1
while N > line:
N -= line
line += 1
#n라인은 n개의 숫자로 이루어짐
#-=으로 무슨 라인에 있는지 알 수 있음
#뺀 것을 저장하므로 해당 라인에 몇 번째인지도 n으로 저
if line%2==0:
numerator = N
denominator = line-N +1
else :
numerator = line - N +1
denominator = N
print(numerator,"/",denominator, sep="")- 1/1
- 1/2, 2/1
- 3/1, 2/2, 1/3
- 1/4, 2/3, 3/2, 4/1
- 홀수 라인 : 분자 감소 / 분모 증가
- 짝수 라인 : 분자 증가 / 분모 감소
- 라인을 먼저 구하고, 그 안에서 순서는 구하면 됨 (여기가 어려웠다)
- n라인은 n개의 숫자로 이루어짐
- -=으로 무슨 라인에 있는지 알 수 있음
- 뺀 것을 저장하므로 해당 라인에 몇 번째인지도 n으로 저장
'기타 > 백준' 카테고리의 다른 글
| 9. 약수, 배수와 소수 (0) | 2023.10.09 |
|---|---|
| 8. 일반 수학 1단계 (2) (0) | 2023.10.09 |
| 7. 2차원 배열(2) (0) | 2023.08.07 |
| 7. 2차원 배열 (1) (0) | 2023.07.18 |
| 6. 심화 1 (2) (0) | 2023.07.14 |
